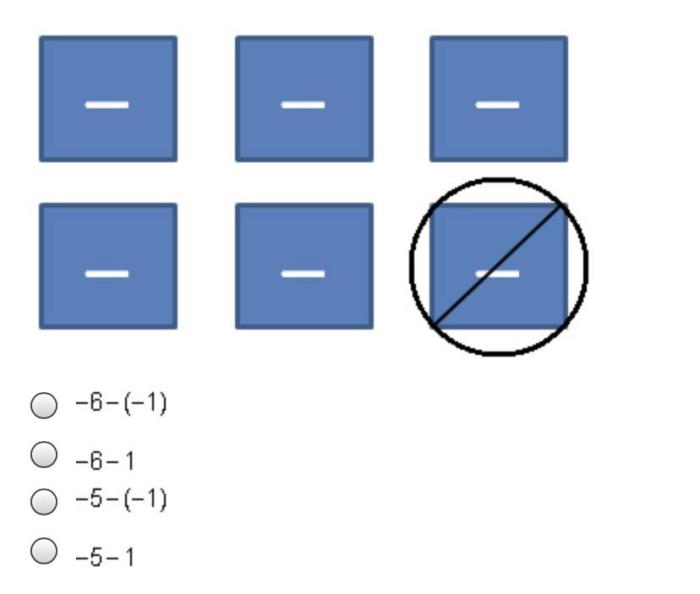
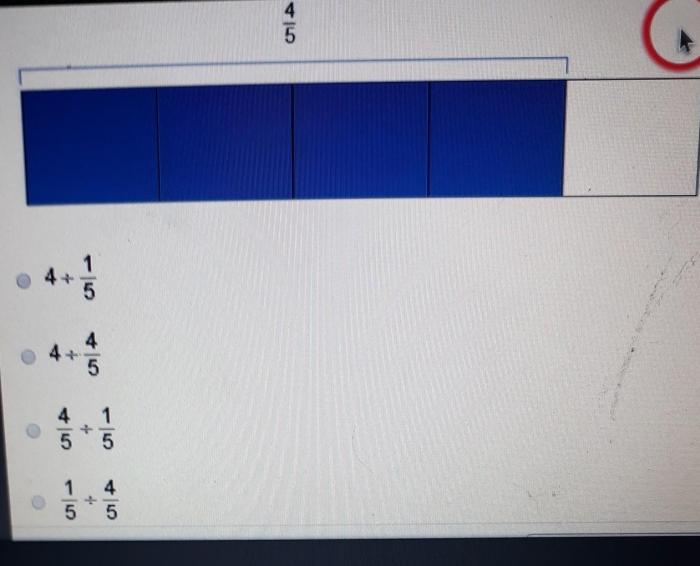
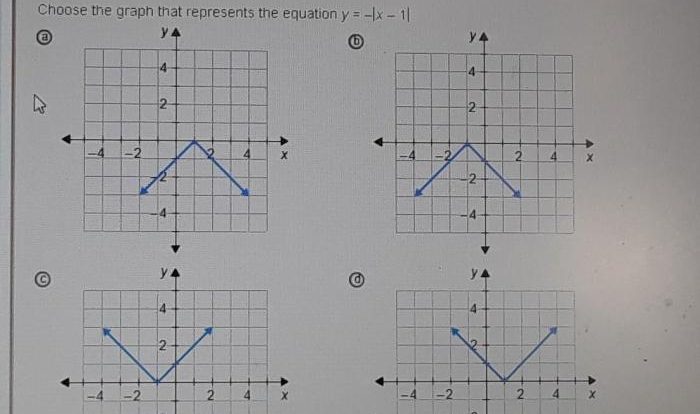
Which expression is represented by the diagram? This question lies at the heart of a fascinating exploration into the realm of diagrammatic representations of mathematical expressions, a topic that has captivated the minds of mathematicians and educators alike. By delving into the visual intricacies of these diagrams, we embark on a journey to decipher their underlying mathematical meanings and unravel the complexities they hold.
Diagrams, with their unique ability to translate abstract mathematical concepts into tangible visual forms, provide a powerful tool for comprehending complex expressions. They offer a bridge between the abstract and the concrete, allowing us to visualize relationships and patterns that might otherwise remain elusive.
Understanding the Diagram: Which Expression Is Represented By The Diagram
The diagram provides a visual representation of a mathematical expression. It consists of symbols, operators, and brackets that are arranged in a specific way to convey the order of operations.
The symbols represent numbers or variables, the operators indicate the mathematical operations to be performed (such as addition, subtraction, multiplication, or division), and the brackets group together related expressions.
The diagram helps visualize the structure of the expression and the relationships between its components.
Expressions and Mathematical Operations
Expressions represented by diagrams can include constants, variables, and mathematical operations.
Common mathematical operations include addition (+), subtraction (-), multiplication (*), division (/), and exponentiation (^). The order of operations (PEMDAS) determines the sequence in which these operations are performed: parentheses first, then exponents, multiplication and division (from left to right), and finally addition and subtraction (from left to right).
The diagrammatic representation reflects this order of operations, with parentheses enclosing expressions that should be evaluated first.
Simplifying the Expression
Simplifying the expression involves removing any redundant or unnecessary components while maintaining its value.
Redundant components may include repeated operations or unnecessary parentheses. By identifying and removing these, the expression can be simplified without altering its meaning.
Simplifying the expression makes it easier to evaluate and understand its mathematical meaning.
Table Representation (Optional), Which expression is represented by the diagram
An HTML table can be used to organize the components of the diagram and their corresponding values.
Each row of the table can represent a symbol, operator, or bracket in the diagram, along with its position and the value it represents.
The table provides a structured way to analyze the expression and identify any redundancies or simplifications that can be made.
Additional Examples and Variations
Diagrams can represent expressions of varying complexity, from simple arithmetic expressions to more complex algebraic expressions.
As the complexity of the expression increases, the diagrammatic representation may also become more complex, with additional brackets and nested expressions.
Variations of the diagram may exist, such as using different symbols or operators, but the underlying principles of representing expressions and simplifying them remain the same.
Expert Answers
What are the benefits of using diagrams to represent mathematical expressions?
Diagrams provide a visual representation of abstract concepts, making them easier to understand and remember. They can help identify relationships and patterns that might otherwise be difficult to see, and they can be used to simplify complex expressions.
How do I determine which expression is represented by a diagram?
To determine which expression is represented by a diagram, you need to identify the symbols, operators, and their positions. You also need to understand the relationships between the components of the diagram and the order of operations.
Can diagrams be used to represent all types of mathematical expressions?
While diagrams can be used to represent a wide range of mathematical expressions, there are some limitations. For example, diagrams may not be suitable for representing expressions that involve complex functions or multiple levels of nesting.