Pythagorean word problems with answers are a fundamental component of geometry, offering a practical approach to understanding the Pythagorean theorem and its applications. These problems engage students in real-life scenarios, fostering critical thinking and problem-solving skills.
This comprehensive guide delves into the intricacies of Pythagorean word problems, providing a clear understanding of the theorem, its applications, and effective problem-solving strategies.
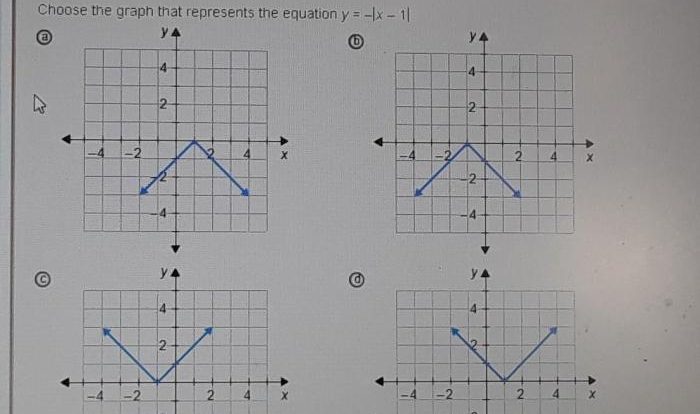
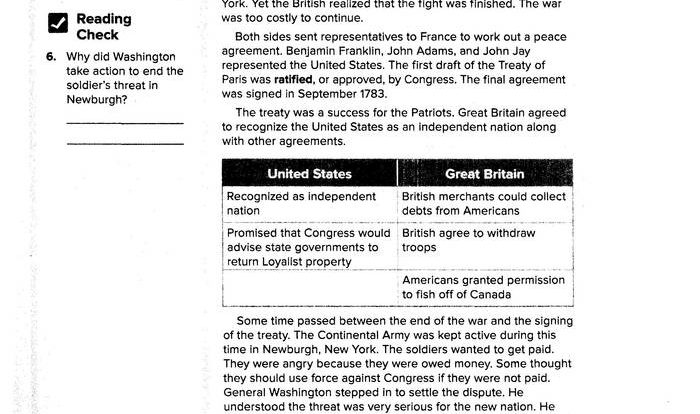
Pythagorean Theorem: Pythagorean Word Problems With Answers

The Pythagorean theorem is a fundamental relation in geometry that establishes a connection between the lengths of the sides of a right triangle. It states that in a right triangle, the square of the hypotenuse (the side opposite the right angle) is equal to the sum of the squares of the other two sides.
The theorem is expressed mathematically as:
a2+ b 2= c 2
where a and b represent the lengths of the legs of the right triangle, and c represents the length of the hypotenuse.
The Pythagorean theorem holds true for all right triangles, regardless of the sizes of their sides. This theorem has numerous applications in various fields, including architecture, engineering, and physics.
Examples of Right Triangles and Side Lengths
Consider the following examples of right triangles and their side lengths:
- A triangle with legs of length 3 units and 4 units has a hypotenuse of length 5 units.
- A triangle with legs of length 5 units and 12 units has a hypotenuse of length 13 units.
- A triangle with legs of length 8 units and 15 units has a hypotenuse of length 17 units.
Relationship Between the Sides of a Right Triangle
The Pythagorean theorem establishes a precise relationship between the lengths of the sides of a right triangle. This relationship can be used to determine the length of an unknown side if the lengths of the other two sides are known.
For example, if we know the lengths of the legs of a right triangle, we can use the Pythagorean theorem to find the length of the hypotenuse. Similarly, if we know the length of the hypotenuse and one leg, we can use the theorem to find the length of the other leg.
Pythagorean Word Problems

The Pythagorean theorem has numerous applications in real-life scenarios. Here are a few examples of word problems that can be solved using the theorem:
Word Problem 1
A ladder is leaning against a wall. The bottom of the ladder is 6 feet from the wall, and the top of the ladder reaches a height of 8 feet on the wall. What is the length of the ladder?
Solution, Pythagorean word problems with answers
We can use the Pythagorean theorem to solve this problem. Let’s assign “x” to represent the length of the ladder. The bottom of the ladder forms the base of the right triangle, which has a length of 6 feet. The height of the ladder forms the height of the right triangle, which is 8 feet.
Using the Pythagorean theorem, we have:
x2= 6 2+ 8 2
Solving for x, we get:
x = √(62+ 8 2) = √(36 + 64) = √100 = 10
Therefore, the length of the ladder is 10 feet.
Word Problem 2
A rectangular garden is 12 feet long and 8 feet wide. If a diagonal walkway is constructed from one corner to the opposite corner, what is the length of the walkway?
Solution, Pythagorean word problems with answers
The diagonal walkway forms the hypotenuse of a right triangle, with the length of the garden representing one leg and the width of the garden representing the other leg. Using the Pythagorean theorem, we have:
x2= 12 2+ 8 2
Solving for x, we get:
x = √(122+ 8 2) = √(144 + 64) = √208 = 14.42
Therefore, the length of the walkway is approximately 14.42 feet.
Word Problem 3
A right triangle has a hypotenuse of 15 centimeters. One leg of the triangle is 9 centimeters. What is the length of the other leg?
Solution, Pythagorean word problems with answers
Let’s assign “x” to represent the length of the unknown leg. Using the Pythagorean theorem, we have:
152= 9 2+ x 2
Solving for x, we get:
x2= 15 2
- 9 2= 225
- 81 = 144
Therefore, the length of the other leg is √144 = 12 centimeters.
Question Bank
What is the Pythagorean theorem?
The Pythagorean theorem states that in a right triangle, the square of the length of the hypotenuse (the side opposite the right angle) is equal to the sum of the squares of the lengths of the other two sides.
How can I solve Pythagorean word problems?
To solve Pythagorean word problems, identify the right triangle and the unknown side length. Then, apply the Pythagorean theorem (a^2 + b^2 = c^2), where a and b are the lengths of the known sides and c is the length of the unknown side.
What are some real-life applications of the Pythagorean theorem?
The Pythagorean theorem has numerous applications in fields such as architecture, engineering, and physics. It is used to calculate distances, heights, and other measurements involving right triangles.